Самое актуальное и обсуждаемое
Популярное
Полезные советы
Важно знать!
5 функциональных и простых сканеров qr и штрих-кодов для андроид
Сканируем QR-код на Android
Основным и наиболее популярным способом расшифровки QR-кодов является использование специальных приложений для Android. В них используется камера телефона, при наведении которой...
Читать далее
12 способов получить максимум от behance
50 лучших бесплатных фотостоков 2021
6 способов посчитать проценты от суммы с калькулятором и без
7 фотостоков для заработка
10 лучших интернет-магазинов дешёвой одежды
27 важных hr-метрик
8 тренажеров для прокачки навыка слепой печати
7 способов узнать какая видеокарта стоит на компьютере
9 мест, где в москве можно бесплатно посмотреть кино
Рекомендуем
Лучшее

Важно знать!
10 важных книг современности, которые стоит прочитать
Список книг, которые должен прочесть каждый
В последнее время стало очень популярно составлять списки 100 самых нужных и популярных книг всёх времен и народов. Каждый такой перечень представляет собой...
Читать далее
33 лучших онлайн-конструктора сайтов, презентаций, визиток и многого другого
7 лучших сервисов для хранения ваших фото в облаке
10 лучших дополнений для яндекс.браузера, которые стоит поставить
10 бесплатных программ для восстановления удаленных данных: файлов, документов, фото
10 лучших онлайн-конвертеров файлов
5 сервисов для сокращения ссылок
6 способов поставить символ градуса при помощи комбинации клавиш и без клавиатуры
4k (разрешение)
15 идей, где заработать первые деньги
Новое
Обсуждаемое
Важно знать!
6 бесплатных онлайн-планировщиков
Any.DO
Программа Any.DO – один из самых популярных планировщиков среди пользователей Android и iOS. Приложение отличается удобным и простым интерфейсом и может синхронизироваться с несколькими устройствами....
Читать далее
25 сильных психологических фильмов, меняющих жизнь
7 лучших деинсталляторов [шпаргалка]
10 лучших дебетовых карт с кэшбэком: рейтинг 2020/2021
7 бесплатных программ для работы c pdf
13 безопасных способов зарядить телефон без электричества
16 советов по съемке фото для instagram
10 каверзных вопросов на собеседовании и как на них ответить
6 лучших способов проверить какая видеокарта на компьютере и как проверить ее на исправность
25 лайфхаков для запоминания дат, имён и не только
Популярное
Актуальное

Важно знать!
11 лучших бесплатных vpn-сервисов для компьютеров и смартфонов
How Website Proxy Works?
Our free web proxy is capable of unblocking blocked websites in your country, region or local network. This is done by sending your request to our proxy servers, which in turn...
Читать далее
17 этапов самостоятельного seo-продвижения вашего сайта [ инструкция ]
7 типов данных, по которым можно найти человека в инстаграме
10 способов подключить мобильный гаджет к телевизору
100 реальных идей, как заработать деньги
2ип
30 лучших книг по психологии, которые стоит прочитать каждому
21 лучший фильм про спорт
6 способов, как полностью удалить яндекс браузер с компьютера с ос windows 10
9 онлайн планировщиков для создания интерьера и плана квартиры
Обновления
 Без рубрики
Обзор поломок компьютера: эффективные методы решения проблем
Без рубрики
Обзор поломок компьютера: эффективные методы решения проблем
В современном мире, где компьютеры стали неотъемлемой частью повседневной жизни, важно осознавать возможные...
 Без рубрики
Как провести качественную пиар-кампанию
Без рубрики
Как провести качественную пиар-кампанию
Имидж компании — это управление репутацией организации. Специалист должен выяснить, как пользователи...
 Без рубрики
Нужно ли начинать бояться биометрии?
Без рубрики
Нужно ли начинать бояться биометрии?
Защита средств идентификации
Мы все знаем, что пароль нельзя никому передавать и следует хранить в...
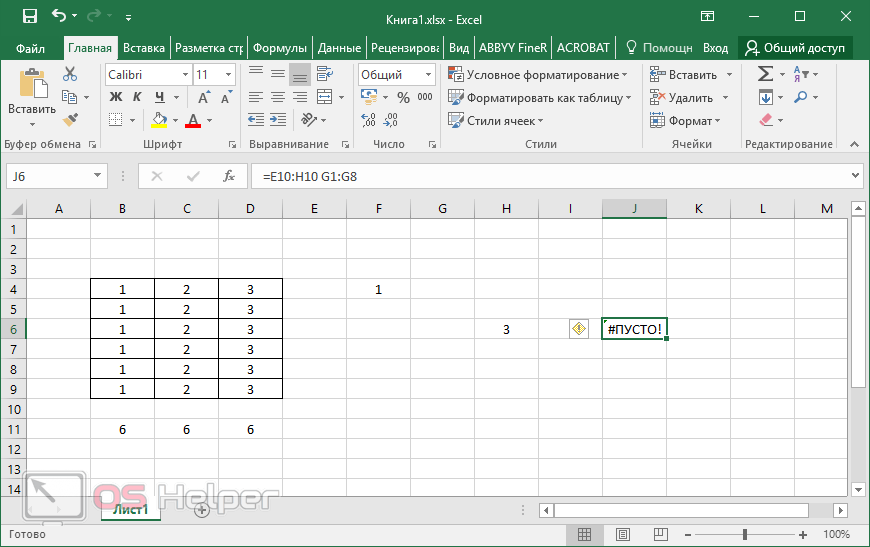 10 популярных математических функций microsoft excel
10 популярных математических функций microsoft excel
Введение
Этот раздел предназначен для пользователей, не знакомых с Excel.
Microsoft Excel – одно из...
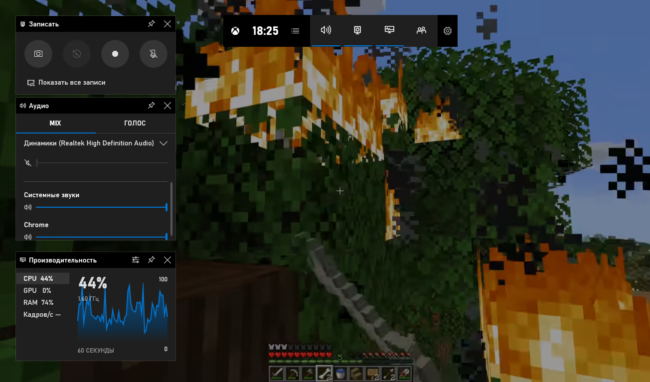 12 лучших программ для записи экрана
12 лучших программ для записи экрана
TinyTake
Бесплатная и простая. Умеет все необходимое. Можно делать скриншоты или захватывать экран в...
 10 лучших фитнес-браслетов с измерением давления
10 лучших фитнес-браслетов с измерением давления
Обзор моделей умных часов с измерением давления и пульса
На основании технических характеристик и отзывов...
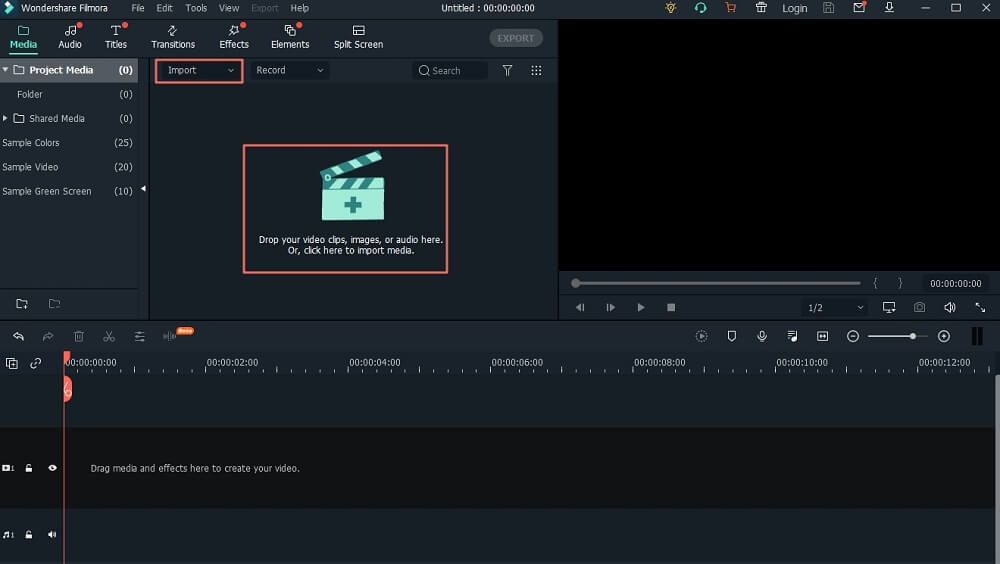 10 лучших бесплатных программ для хромакея в 2021
10 лучших бесплатных программ для хромакея в 2021
Делаем чёткими контуры на волосах после зелёного фона
Так здесь у нас все хорошо, но в волосах это так...
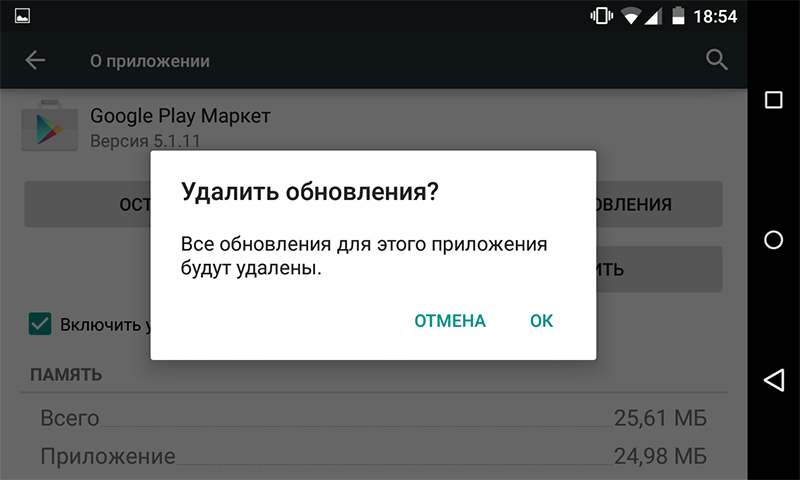 3+ fixes for the fix error code 907 in the google play store
3+ fixes for the fix error code 907 in the google play store
So What Does “Error 907” Even Mean?
Simply put: it’s a bug in the Google Play Store. “Error 907” can...
 36 лучших приложений для android, которые стоит установить
36 лучших приложений для android, которые стоит установить
Мессенджеры
Общение через смартфон для многих стало неотъемлемым атрибутом в жизни. Мессенджеры позволяют...
 50 невероятных идей для хобби в декрете
50 невероятных идей для хобби в декрете
Репетитор
Эта работа также подойдёт тем женщинам, которые хорошо владеют иностранными языками или играют...
 10 бесплатных онлайн-курсов по финансовой грамотности и инвестированию
10 бесплатных онлайн-курсов по финансовой грамотности и инвестированию
Сайты для улучшения уровня образования в сфере финансов
Некоторые сервисы предлагают онлайн уроки, где...
 4к-контент для ultra hd телевизоров: где его можно найти
4к-контент для ultra hd телевизоров: где его можно найти
Что такое 4K
В разных контекстах 4К называют разрешения, имеющие по горизонтали около 4000 пикселей....